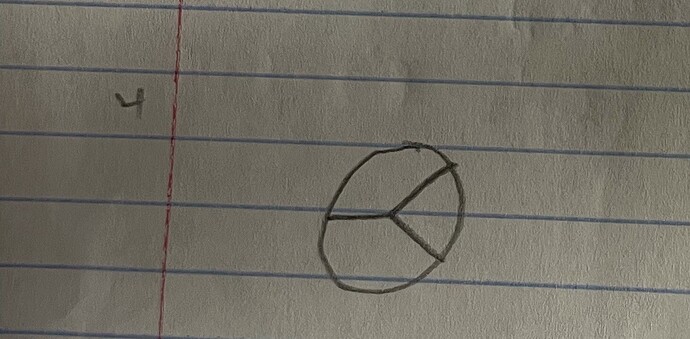It may be because of how lines can bisect one another. If a line goes straight up and down the center, and another goes left to right in the center, then that’s nine or so different possibilities for how we can draw that, since any line can end where they intersect.
My Further Calculations accounted for that. It includes all possible combinations of a line between two points. The possible lines include top-centre, centre-bottom, and top-bottom, and the combinations account for all possible combinations of these, even the redundant ones.
And what about lines that don’t intersect at the center?
It takes into account any possible line between any of the two points. This could be a “half-length” line from the perimeter to the centre, or it could be a “full-length” line between any two perimeter points; the formula doesn’t differentiate.
The formulae account for any line between any two points (with the exception of lines that would be colinear with the body of the hexagon), and calculates every possible combination of these lines (and the circles) being “on” or “off”, regardless of whether the lines intersect and/or are colinear.
It could be compared to a coin flip. Imagine flipping a coin for each line and circle, with heads meaning that the component is present, and tails meaning it’s not. Generating a circular glyph would require 45 coin flips (one for each line and point), and the formula accounts for every possible combination.
To clarify, 3x10^23 was just for the circular glyphs, not for the hexagon glyphs.
I can explain the math, but sorry in advance for the wall of text.
So my first thought was what you said, treat every line/circle as on or off, then calculate the total combinations.
Since there are 9 circle bits and 16 line bits, that leaves 2^25 possibilities.
However this doesn’t take into account lines that stop partway across the circle because of an intersection.
Consider just the possibilities of lines 1-5, 8-6, and 7-3.
Looking at them as bits gives us 2^3 possibilities
However, that doesn’t take into account these legal glyphs
Next idea. Instead of only counting each line as on or off, consider the order that they are added to the circle.
That is, we add a line A, then add another line B which would stop when it intersects the first line, and this would be glyph AB.
If we reverse the order we add the lines, we get glyph BA
This accounts for all the glyphs shown so far, and can be calculated as permutations.
However, we also must consider that lines can start from either edge of the circle, effectively doubling the number of lines in the situation.
So for these three lines, we have 6 possible starting points, of which we are sampling three, where the order they are sampled in matters. The permutation of 6 take 3 is
P(6,3) = 6!/(6-3)! = 120. That’s the number of combinations exclusively for these three lines when all are active at once. We also have to add
P(6,2) and P(6,1), and the 9 glyphs we had before.
Do this for all 16 lines with the equation Σ(i=0, 16) P(32, i), and the total is a staggering 13,359,435,408,855,851,031,425 ~ 1.3x10^22.
This is not including the hexagon bordered glyphs.
This method does have a small number of overlapping cases, but it could be used as an upper bound, if it wasn’t for the fact it was also wrong.
This pattern fails to take into account this glyph, since there is no ‘first’ line in this glyph.
It also fails to take into account glyphs like this, since the center line doesn’t start at an edge. I’m not sure if this is a legal glyph,
but it looks cool, and similar to what we have seen, so I’m gonna assume its legal.
At this point I realized the total number of possible glyphs was a function not of the number of lines and circles, but of the number of intersections of the lines.
If we take all the intersection points, that is, all the points a line could start or stop within the circle, we end up with 40 points.
I took the liberty of combining several intersections that are very near each other into the same point, since that’s how I would guess a language would actually work.
By manually inspecting all the legal sublines within this grid we can establish 84 subsections of lines.
Using this number, plus the 9 circles, we can finally calculate a true upper bound to the number of glyphs. By considering every subline as either on or off, we can be sure there are less than 2^93 legal glyphs.
This is an incomputably large number, so it would be impossible to check which glyphs are legal even by computer. So I went with the next best thing, statistical analysis.
Writing a quick python script to generate possible glyphs in a uniformly random way, we can then calculate some sample of legal and illegal glyphs, find how many are actually legal, and extrapolate that percentage to the entire population.
I considered an illegal glyph any one that had a line connecting to the edge of the circle where a smaller circle also was, or any time a line ended on a non-intersection. Like these.
Running the script for a few minutes, we can generate half a million glyphs. Of these, four were legal, or 0.0008% of all possible glyphs.
This estimate has a margin of error of 3.5155495x10^-40, as a 95% confidence interval.
This gives us a total of 3.1691265*10^23 legal glyphs.
The real danger is, with a 95% confidence interval, there’s a 5% chance the true value is outside the MOE. I could probably run it through a more precise CI as well if people wanted.
Please let me know if you see a mistake in my math. I’m in to deep to get it wrong now lol