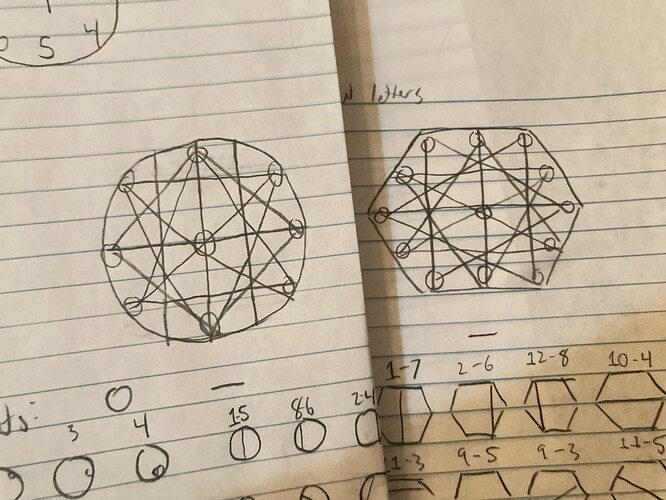Matoran alphabet theory (like analysis, not explanation)

KDNX · February 9, 2022, 2:53am

I’ve had a little bit of a… fixation on the Matoran alphabet the last few hours. I’ve been analyzing the 57 canonical glyphs and I’ve broken them down into “theory sheets” and I’m working on design sheets for the two variants of the alphabet (circular octet style and hexagonal duodecad style). Let me illustrate to you what I mean.

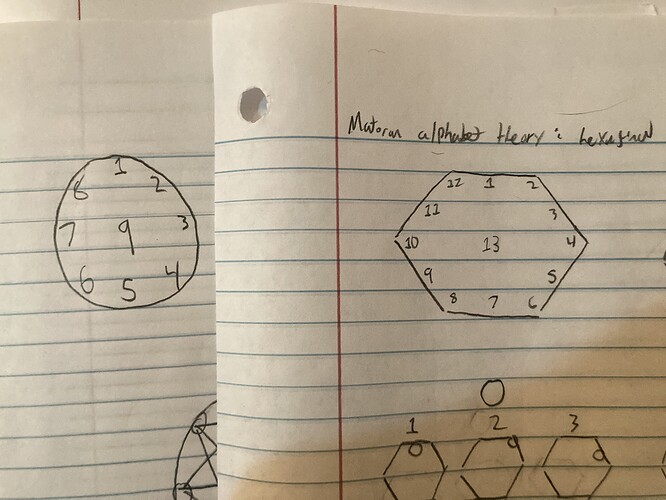
The two styles of Matoran alphabet are circular octet and hexagonal duodecad. This refers to the outer shape of the glyph and the number of “positions” within the glyph (to be explained). Nepycros helped me come up with the theory that the circular octet style is a younger simplification of the hexagonal duodecad style, which is older and more formal.

Glyphs are made up of the outer shape and a number of “components”, which are circles and lines. Lines never intersect a circle (unless the glyph is a number, which have different position rules), and if a line intersects a line, it can end there. A line never ends without touching the edge of the glyph or another line.

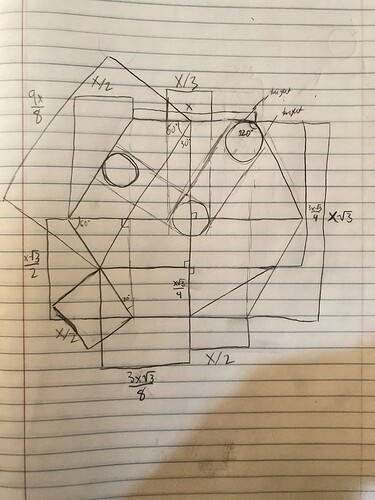
Now, the positions. We’ll begin illustrating what I’m talking about with the aforementioned theory sheets. The glyphs can be divided into eight or twelve positions, like so:

The positions represent a point within the glyph where a line or circle can be placed. The 9th position (for the circular octet style) and the 13th position (for the hexagonal duodecad style) represent the point where numbers receive their central circle.

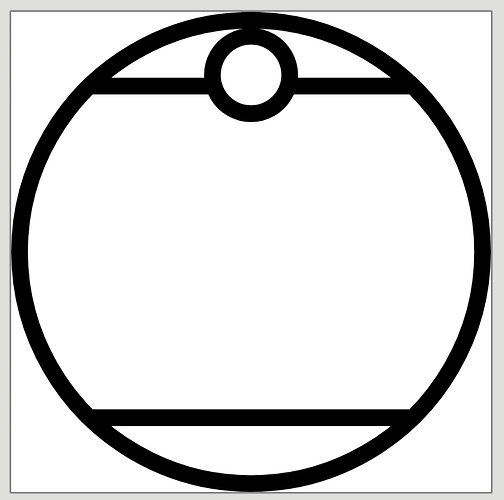
Next, we have the “ur-glyphs”. These are glyphs made up of all attested positions of line and circle.

Each circle and line can be named by the position it occupies, with circles receiving a designation of one number and lines receiving two hyphenated numbers, denoting their start and end points, right to left (and top to bottom if they are vertical).

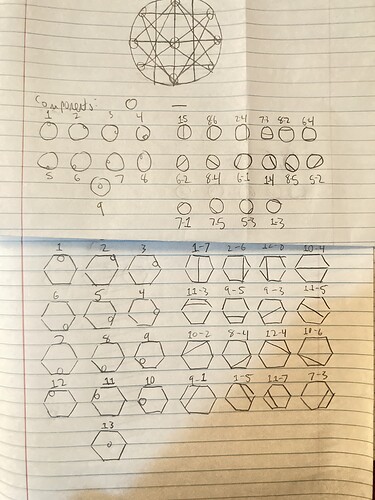
Given the 57 glyphs, we have, for both styles, sixteen line possibilities (including mirrored versions of attested patterns, such as 7-5 and 1-3, which are mirrors of 7-1 and 5-3, which are attested in the glyph for Ö). The circular octet style has nine inner circle positions, including the central circle for numbers, and the hexagonal duodecad style has thirteen including the central circle. It’s notable that the hexagonal duodecad style has many more unattested line possibilities than the circular octet style.

With all of this data and info, I hope to be able to determine the number of possible glyphs. Unfortunately, I don’t think it’d be easy to calculate this with a simple math equation, the number of changing variables makes it unfeasible. Of course, it’s also pretty unfeasible to write out every possible glyph, so we’ll see what I can come up with.

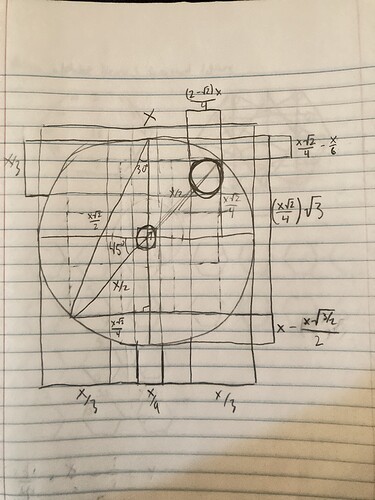
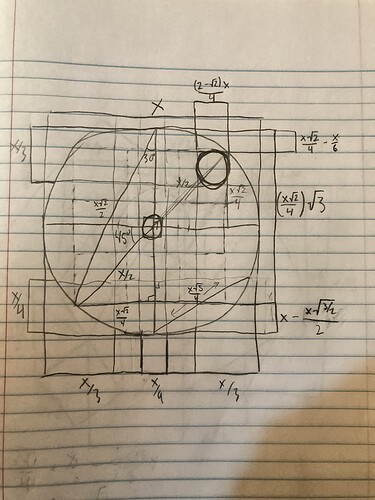
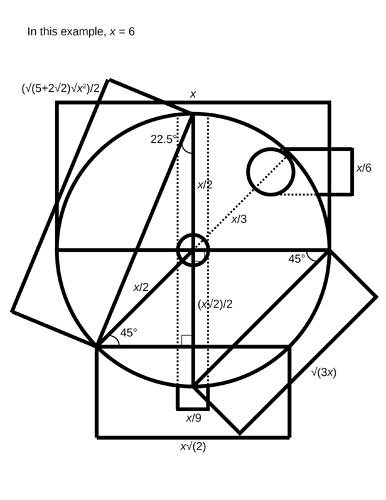
The final fruit of all of this labor is the “design sheet”, a first-pass mathematical diagram I came up with for how an ideal circular octet glyph would look. I’ve calculated a lot of the lengths and ratios in here, and I have plans to digitize it and clean it up. I also want to make a version of this for the hexagonal duodecad style, but it’d be difficult to do that by hand.

Thanks for reading this diatribe. I hope to update this over the next few days with the digitized design sheet, the hexagonal design sheet, and some examples of never-before-seen glyphs.

Atobe_Brick · February 9, 2022, 3:04am

You know you’re a bionicle fan when:

I’ll keep an eye on this topic to check out your findings

Winger · February 9, 2022, 3:06am

We went from clocks to satanic symbols to geometry.

And they say this isn’t a Bionicle forum.

KDNX · February 9, 2022, 3:39am

Well, here’s the design sheet for the hexagonal glyph. This was easier than I expected. Also included is an updated version of the circular one, which was missing a line.

All that’s left to do is determine the number of unique glyphs we can have.

Enbeanie · February 9, 2022, 8:54am

That may be an understatement./s Good work on this!

Rukah · February 9, 2022, 1:34pm

Oh man you’ve done your work on this. I’ll be interested on seeing what else you come up with.

Macantonio · February 9, 2022, 4:05pm

The math for all glyphs should actually not be too hard for this, I might have time to run the numbers later today.
For the circle glyphs we can calculate the combinations by summing Choose 25, i from i = 1 to 25.
Sum(25, i=1, C(25,i)).
Similarly for the hexagon glyphs we can calculate the combinations by summing Choose 29, i from i = 1 to 29.
Sum(29, i=1, C(29,i)).

KDNX · February 9, 2022, 4:12pm

That wouldn’t be the whole equation though, because we need to be able to account for glyphs that contain both circles and lines, and account for the fact that lines should not intersect circles, and the fact that a line can be ended by another line.

Macantonio · February 9, 2022, 4:27pm

Ah, yeah didn’t think of the lines intersecting circles part. I still think the calculation can be done with a few tweaks tho, maybe you would need to modulate n in choose(n,k) to account for intersections at different sample size choices?
Or calculate total possible invalid glyphs and subtract from the total.
I’d have to think about it a bit.
Edit: looking at an upper bound of over ~500 million glyphs though… definitely don’t draw them all.

KDNX · February 9, 2022, 8:35pm

Here’s the digitized design sheet, with some updated, more accurate math, as well as some tweaks to positions.

EDIT: forgot to square root the length of the 6-1 line

KDNX · February 10, 2022, 5:01pm

I’m doing one-by-one analyses of each character now. I’ve noticed something interesting about the Russian letter Ё: it necessarily has a line overlap a circle unless the circles are drawn extremely small.

Here is how I’ve chosen to render it:

Winger · February 10, 2022, 6:45pm

Macantonio · February 12, 2022, 4:39am

Upon further exploration, I can say with 95% confidence that the total number of legal glyphs is 3.169 x 10^23
For reference, that’s around 3 times the number of atoms in a gram of water.

KDNX · February 12, 2022, 4:45am

Darn. Guess I won’t be drawing them all up then, lol. Thanks.

Macantonio · February 12, 2022, 4:56am

To be fair, the number of cool looking ones is actually pretty low (compared to 10^23):
But when you consider every variation of these lines, what is technically possible grows really fast.

GoodGuy2006 · February 12, 2022, 5:03pm

huh, i never suppose i thought about how matoran would have to be adapted to other languages

i’m scared to see the japanese matoran writing system

KDNX · February 12, 2022, 6:52pm

I bet I could put together a Matoran hiragana / katakana syllabary pretty easily. Now Chinese, on the other hand…

Winger · February 13, 2022, 2:37am

And that’s where all the different possible glyphs come in.

Atobe_Brick · February 13, 2022, 3:17am

Wow. That’s way way way more than I had expected…

TheJerminator · February 13, 2022, 4:10am

I’m not sure if I agree with this.

Just for the sake of this comparison, let’s assume that lines are allowed to intersect circles. This massively simplifies the calculation, since it makes each line and circle completely independent; each one is either “on” or “off”.

For the circular glyphs, there are 9 circle locations and 16 line locations for a total of 25 possible components, each of which can either be “on” or “off”. The total number of combinations can then be expressed as 2^25, or approximately 3.35*10^7.

A similar calculation for the hexagonal glyphs gives 2^(13 + 16) = 2^39, or approximately 5.5*10^11.

In the grand scheme of things, the number of potential circular glyphs is negligible when compared to the total number of hexagonal glyphs; all in all, there are “only” approximately 5.5*10^11 possible combinations of the lines and circles shown here.

And keep in mind, that’s ignoring all of the rules about intersection and other limitations; the number of legal glyphs will be much lower.

Further Calculations

Just for fun, let’s oversimplify things even further. Let’s assume that lines can be drawn between any two circle locations, with certain exceptions for some lines in the hexagonal glyphs. I will be excluding the lines between adjacent points on the perimeter, as well as those between adjacent corners of the hex, as they would be colinear with the sides of the body. With these loosened criteria, there are now 36 possible lines for the circular glyphs, and 60 for the hexagons (78 possible lines, minus the 12 lines between adjacent points, minus the 6 lines between the corners). The calculations now become this:

Circular: 2^(9 + 36) = 2^45 ≈ 3.5*10^13

Hexagonal: 2^(13 + 60) = 2^73 ≈ 9.4*10^21

Even with these massively simplified calculations, ignoring all of the rules for a “legal” glyph, I cannot find a way to obtain a number of glyphs with an order of magnitude of 23.

Despite all of my assumptions, and ignoring the “glyph rules”, my answers are still far smaller than yours. How did you get your answer to the power of 23?

EDIT: I just realized my Further Calculations could actually ignore even more lines, resulting in even fewer combinations; having a line run from the top left point of the hex to the center, and then having another line from the center to the bottom right corner, would be functionally identical to just having a line from the top left to the bottom right.