Yes another one of these is finally here.
This time we are going to look at the physical strength of our best boy Taipu.
Famously in MNOG, he is depicted lifting and tossing away giant boulders bigger than he is, so I was interested in how much strength this would require on his part.
But before we get into the actual analysis, let’s establish few things. This is an analysis of a strength of a Matoran, one of the weakest sapient species of MU. However there are more specifics to consider: Taipu is an Onu-Matoran who are said to be stronger than most other types thanks to their elemental affiliation. On the other hand the Matoran of 2001 are deminutive and weaker than normally thanks to the adverse effects of Makuta’s pods. And on the third hand, out of the whole population of Onu-Matoran with afformentioned characteristics, Taipu is the strongest individual specimen. We do not know how all of these factors affect the overall strength, but they are important to keep in mind.
With that out of the way, let’s get to business!
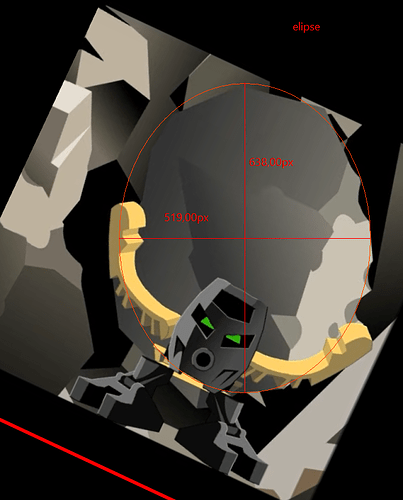
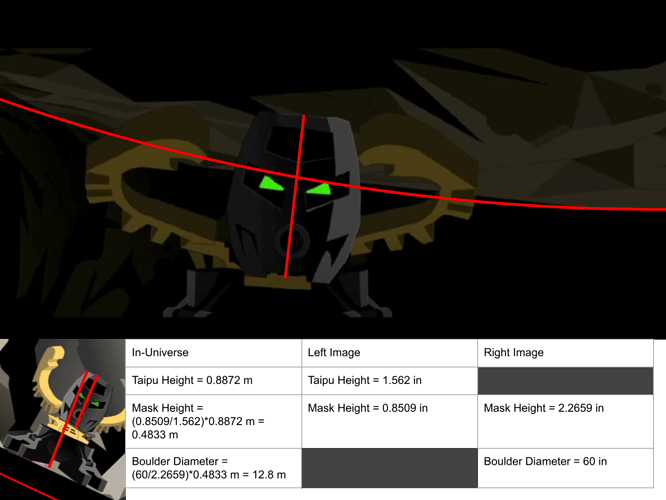
I took equivalent screenshots of the scene in question in scale to eachother to be analysed. I used one to measure the pixel height of Taipu and the other to measure the boulder. The latter was a bit tricky because it has such an irregular shape - I eventually settled on a best fitting elipse where chunks of rock outside the boundary approximately corresponded to the empty space inside. Thanks to this I got the height and width of the boulder and I assumed the width value in place of thickness to keep as close to perfect ellipsoid as possible:
The reason I had to use two pictures was that one has the entire boulder, but in the other, Taipu is standing upright instead of squat. Because the perspective does not change between them and the screenshots have identical sizes, their resolution is identical as well.
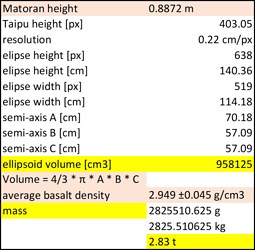
And resolution is what I calculated next. Using Taipu’s pixel height and a height of 2001 Matoran I calculated in one of my earlier analyses (0.8872 m, or 88.72 cm), I was able to determine that the resolution of the pictures is 0.22 cm/px.
With this in mind, it is easy to convert pixel values to centimeters, which is what I did for the boulder.
The results indicate the following:
height: 140.36 cm
width: 114.18 cm
thickness: 114.18 cm
Ok, so next we need to figure out the volume. The formula for ellipsoid volume is: Volume = 4/3 * π * A * B * C
where A, B and C are semi-axes of the three dimensions, so just divide those numbers by two.
Plugging the numers in, we get a final volume of 958125 cm3.
Nice!
Now we can proceed to the final step which is to calculate its mass. But for that we need to know the density of the rock the boulder is made of. Obviously we do not know what type of rock this is and it may or may not be protodermic, but there is a pretty good educated guess I am comfortable with…
Looking at the rock’s appearance and texture it appears it could be basalt:
Basalt makes a lot of sense, not only thanks to its look, but the setting - Mata Nui is a volcanic island and basalt is a volcanic rock that is most predominant on Earth. We also know that basalt was among many polynesian inspirations of early Bionicle. This is the best we can probably get.
The average density of basalt is 2.949 g/cm3.
Now we can finally get to the value we were looking for. The total mass of that basaltic boulder Taipu is lifting is a whopping 2825510.625 g, or 2.83 tons!
Taipu is lifting almost 3 tons like it was nothing and proceeds to lift it all the way above his head and toss it away like a mere pebble!
He really is a strong guy.
…
Of course there is more that can be deciphered, but this is where I would ask you readers to add your skills to the mix. Since I wanted this one to be interactive I have the following task for you: calculate the distance the thrown boulder travelled.
Here is some additional data:
-
The first boulder (which is thrown) has the same shape and thus mass as the one analysed here.
-
Right before being thrown its lowest edge is situated right at the head height of Taipu which is afformentioned 88.72 cm and the boulder is held horizontally instead of vertically like was the case in this analysis (so the elipse is on its side).
-
Assume the boulder flies in straightline and there landscape is flat. Also assume earth-like gravity for this (even though it wouldn’t really be the case).
-
And lastly, the time the boulder remains airborne is 0.83 seconds (25 frames between leaving Taipu’s hands and the first shake of the screen indicating landing, 30 fps video).
We don’t know the force at which the rock was thrown, but if there is a way to calculate its descent without it, then perhaps that can be calculated later. I am interested in what all of you will cook up!
PS:
Here is the table with values from my analysis.