A question as old as the stars themselves…
I did not plan to cover this topic in my analysis series because it was already covered by others, most notably by 742mph on BZP, and by @RahiWatching over here on TTV message boards. Especially RahiWatching did a particularly outstanding job of trully diving deep into many aspects and details of the physics.
What led me to change my mind is that both afformentioned analyses contain some factors which I consider eihter inaccurate or distracting from answering the core question: “What is the best estimation of the actual size of Spherus Magna and its fragments, as presented in the Bionicle story.”
The initial analysis by 742mph from 2012 has a very nice base idea and procedure, but uses either suboptimal or outdated data.
RahiWatching’s analysis, while much more comprehensive and robust, decides early on to sacrifice story accuracy in favor of greater realism and cross-consistency within chosen dataset. It is much more concerned with working out a functional planetary system than finding out the true answer based on objective evidence. (The appendix of the paper does eventually express opinions on the actual SM size, but I was not satisfied with the methodology).
So I eventualy decided to do this analysis myself. Can I bring something new to the table? Can I come to a more accurate answer than my peers? Let’s find out.
Starting from the beginning, I wanted a general idea of how I would approach this and after some contemplation I decided that an approach similar to that of 742mph would be the best - and perhaps the only good way to do this considering all three of us analysts ultimately settled on similar methods.
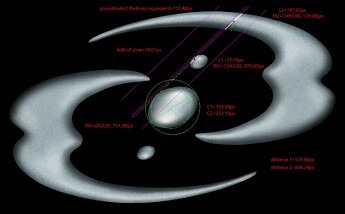
The approach is to use the picture of Mata Nui falling into Aqua Magna (from Mata Nui saga) as a measure of AqM’s planetary diameter. This method relies on the fact that GSR has a known size of 12 192 km, thus size of any object next to it can be estimated using pixel measurements.
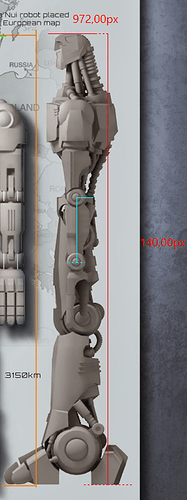
Just like in my forerunner’s case, I decided to use the robot’s lower arm, which is perpendicular to the line of sight of the observer. By measuring its length in pixels and fitting AqM horizon to a circular shape, one can determine the circle’s and thus AqM’s diameter.
For that of course, we should start with determining the length of the lower arm. My forerunner used a comic picture coupled with some guesstimation of the robot height to arm length ratio, but I knew I could do better.
Why guess the ratio from an artist’s interpretation of the robot in a dynamic pose no less, when you have a solid 3D template this art was based on, standing upright, available to you? The original of this picture contains two views of GSR, but I chose the side view because it included the head crest (the highest point of the robot):
Another advantage of my take on this matter is that I have access to superior measuring tools than both of my forerunners, which enables me to achieve far greater accuracy. I also measured the arm length from centerpoints of the joints.
Ok, so this is the arm length of the robot:
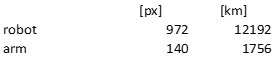
1756 km lower arm. We can see now that 742mph has overestimated the arm length (2562 km).
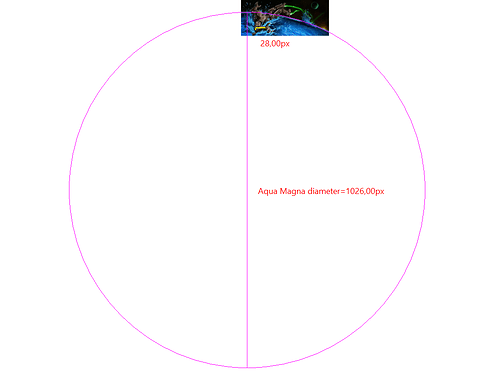
Now we can move on to the picture of GSR falling where we make another line connecting the joints of the lower arm. We also measure the diameter of AqM:
With this data, the diamter of the AqM is:
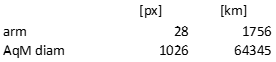
Diameter of 64 345 km.
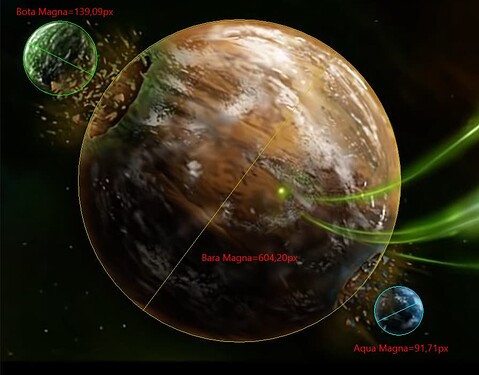
Now that we know that, we can compare diameters of the other three planets and make claculations. Note that diameters of Bara Magna and Spherus Magna are identical because AqM and BoM left holes while maintaining spherical shape of the main planet. For this, we have yet another MN saga picture:
This is essentially all we need when we already have a known AqM diameter. By plugging the diameter numbers into equation for spherical volume and multiplying by average density of the Earth (5515 kg/m3), we get the actual masses of the planets. When compared to celestial bodies of our solar system we unsurprisingly find out that they are massive!

We see that out of the three Bionicle planets, only Aqua Magna is overtaken in mass by the largest planet of our own solar system Jupiter, with Jupiter being 2.5X more massive. Other than that, every planet is way more massive and only the sun can remain competitive. Even still, the original Spherus Magna constitutes 1/18th of the Sun’s mass, which is insane for a terrestrial planet. Obviously such planet could not exist in our universe, but the rules of fiction allow this.
When we compare this result with 742mph’s analysis, we can see that my forerunner overestimated the SpM size, stating it was 11X larger, when in reality it is only 3X difference (which is still huge).
Of course, the calculated mass of SpM should be considered an underestimation. A rocky planet of such size certainly wouldn’t have density equal to Earth as I have assumed here, it would presumably be bigger if it were possible for a planet like this to exist. Unfortunately, I lack expertise to even begin to estimate how density would increase with the volume - but if there’s someone who could contribute their knowledge you are more than welcome to make input.
Nevertheless, as you can see, I have also calculated the surface gravity of SpM with assumed Earth density and it seems to be 326.8 m/s2. When compared to Earth’s gravity of 9.81 m/s2, we see that it is 33.3X larger.
I found a study which concludes that humans would need to be in peak athlete condition to move in just 4X greater gravity, meaning Spherus Magnans have to be ridiculously strong - no wonder they evolved metallic bones. And remember this is underestimation…
Just to paint a picture, surface gravity of SpM is even greater than that of the Sun (274 m/s2)!
…
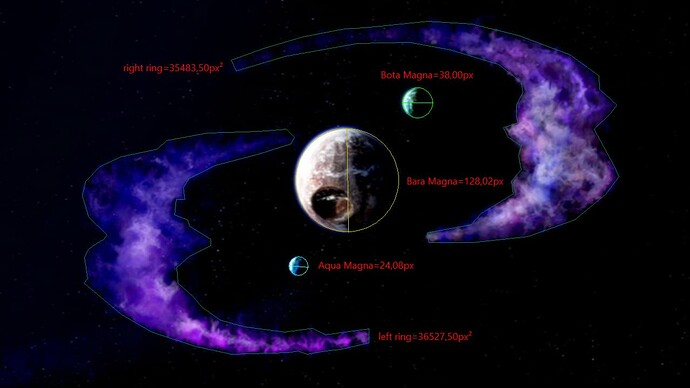
I could end it here, reasonably confident that I have improved on previous answers to this question. But I decided to go a step further and do something none has dared before - calculate the size and mass of Spherus Magna’s rings. For this I have used a shot from Legend Reborn movie along with depictions of the UDD symbol. Getting the 2D area of the rings was trivial:
But to calculate their volume I needed the thickness. I knew there was at least one animation showing the camera passing through the UDD symbol in 3 dimensions and also remembered that a wiremesh of the 3D model was partially depicted in one of the style guides:
Assuming that Great Beings were accurate in modeling this symbol after the post-shattering Spherus Magna, I wanted to compare the thickness of the rings to the diameter of one of the planets. This proved far too difficult however because of the changing angles and perspective of the camera. I set out to do a complicated approximation of the camera’s position and calculation of the percieved size change based on distance, but I concluded that the room for error was far too great for something so laborious and instead opted for simply guesstimating a cross section where the height of the ring’s arm equates its thickness, and I took an average of the middle dot’s diameter to be SpM/BaM diameter and calculated the actual thickness in km based on that (So only green shapes in the second picture were used).
I arrived at afollowing ring volumes in km3:

To calculate the mass, I assumed the rings are made of ionized gas just like nebulae in our universe. The purple number you see is an average density of Ring nebula and the overall mass I have calculated for both rings. Because nebula density is extremely low, the mass turns out to be equal to just 2.2 Eiffel towers spread out across an enormous space. Considering though that actual nebulae are still much larger than this, I suspect that SpM rings are more dense - then again I’m not sure if nebulae this small could realistically maintain this luminosity.
For fun, I decided to assume that the rings have similar composition to the rings of Saturn (even though they are explicitly described as gas rings in the source material) and this time I arrived at far larger numbers:
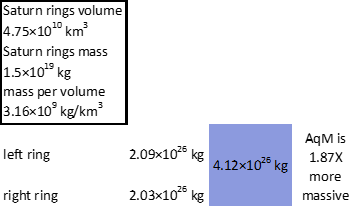
Turns out the rings would have mass approaching that of AqM, though it would still be 1.87X more massive.
Neither of these two interpretations wouldn’t have significant impact on the mass of Spherus Magna though as it is several orders of magnitude more massive.
At this point I am satisfied with my findings, but this is not necessarily the end. I’m sure if more community members with various areas of expertise came together, we could work out much more. For example, I would be interested if it is possible to take an educated guess as to the element composition of Spherus Magna based on the (percieved) wavelength spectra of the rings. Even if it were very rough guess work, any attempt would be interesting.
I’m happy to hear any feedback.
Here is the final size comparison for Earth, Aqua, Bota Magna, Jupiter, Bara/Spherus Magna and Sun.